前缀与差分模版

前缀和与差分

前缀和

题目：

输入一个长度为 n 的整数序列。

输入一对 l,r。输出原序列中从第l 个数到第 r 个数的和。

例如：

• 整数序列为：2 1 3 6 4
• 输入1 2 输出3
• 输入1 3 输出6
• 输入2 4 输出10

思路：

• 原数组:a[1],a[2],a[3]...
• 前缀和数组：s[1],s[2],s[3]...
• s[1]=a[1]
• s[2]=a[1]+a[2]
• s[3]=a[1]+a[2]+a[3]
• 前缀和数组S[i]=a[1]+a[2]+a[3]...+a[i]
• 数组a[l,r]的和为S[r]-S[l-1]=a[l]+...+a[r]
• 规定S[0]=0,S[i]=S[i-1]+a[i]

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=100010;

int n,l,r;
int a[N],s[N];

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	
	for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
	
	scanf("%d%d",&l,&r);
	printf("%d\n",s[r]-s[l-1]);
	return 0;
}

如何只使用一个数组存储：

for(int i = 1; i <= n; ++i)
{
    scanf("%d", &arr[i]);
    arr[i]+=arr[i-1];
}

二维前缀和

img

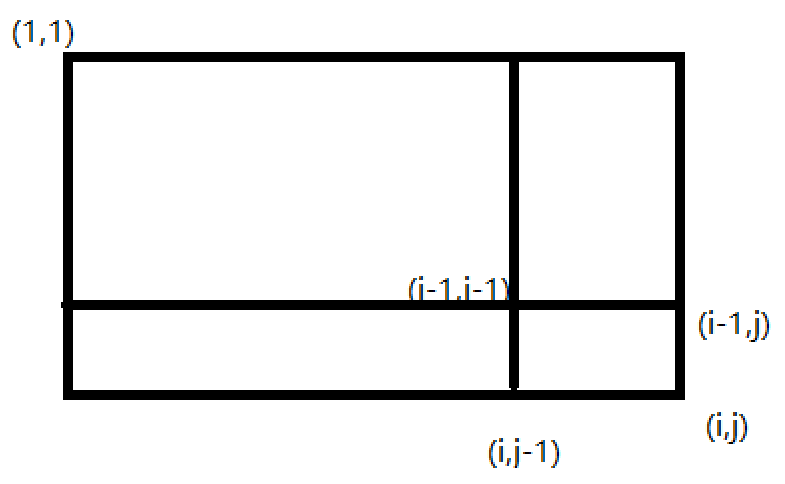
思路：

二维前缀和预处理公式：s[i,j]=s[i,j-1]+s[i-1,j]-s[i-1,j-1]+arr[i,j]代表的是(1,1)到(i,j)的元素之和

矩形(x1,y1)到(x2,y2)的所有和为：s[x2,y2]-s[x2,y1-1]-s[x1-1,y2]+s[x1-1,y1-1]

代码：

#include<bits/stdc++.h>
using namespace std;

const int N=1010;
int n,m,q;
int a[N][N],s[N][N];

int main(){
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&a[i][j]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];//前缀和公式
	
	while(q--){
		int x1,y1,x2,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		printf("%d\n",s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]);//输出和
	}
	return 0;
}

差分

题目

输入一个长度为 n 的整数序列。接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r]之间的每个数加上 c。请你输出进行完所有操作后的序列。

• 输入格式：第一行包含两个整数 n 和 m。第二行包含 n 个整数，表示整数序列。接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。
• 输出格式：共一行，包含 n 个整数，表示最终序列。

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例:

3 4 5 3 4 2

思路

原数组:s[1],s[2],s[3]

差分数组:a[1],a[2],a[3]

a[1]=s[1]-s[0]

a[2]=s[2]-s[1]

a[3]=s[3]-s[2]

差分数组公式：a[i]=s[i]-s[i-1]

事实上：原数组为就是差分数组的前缀和数组

s[1]=a[1]

s[2]=a[1]+a[2]

s[i]=a[1]+...+a[i]

将[l,r]区间内的每一个数都加上一个常数C,那么对于差分数组的处理是a[1]+=c,a[r+1]-=c

代码

#include<bits/stdc++.h>
using namespace std;

const int N=100010;
int n,m;
int a[N],b[N];
void insert(int l,int r,int c)
{
	b[l]+=c;
	b[r+1]-=c;
}
int main(){
	scanf("%d%d",&n,&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	
	for(int i=1;i<=n;i++) insert(i,i,a[i]);
	
	while(m--){
		int l,r,c;
		scanf("%d%d%d",&l,&r,&c);
		insert(l,r,c);
	}
	
	for(int i=1;i<=n;i++) b[i]+=b[i-1];
	
	for(int i=1;i<=n;i++) printf("%d",b[i]);
	return 0;
}

二维差分

思路

将(x1,y1)到(x2,y2)内的每个元素都加上一个常数c,对于矩阵b来说有：

b[x1][y1]+=c

b[x2+1][y1]-=c

b[x1][y2+1]-=c

b[x2+1][y2+1]-=c

代码

#include <iostream>
using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            scanf("%d", &a[i][j]);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            insert(i, j, i, j, a[i][j]);

    while (q -- )
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];

    for (int i = 1; i <= n; i ++ )
    {
        for (int j = 1; j <= m; j ++ ) printf("%d ", b[i][j]);
        puts("");
    }

    return 0;
}