CF1600分刷题记录有意思的题目
Parsa's Humongous Tree
https://www.luogu.com.cn/problem/CF1528A
题面翻译
多组数据 ( 组)
给你大小为 的一棵树, 号节点有权值范围 ,让你对每个节点赋予一个权值 ,使得每个节点权值都在规定的范围里并且对于每条边 , 最大,并求出这个最大值。
,时限 ,空限
Translated by @ZCPB
题目描述
Parsa has a humongous tree on $ n $ vertices.
On each vertex $ v $ he has written two integers $ l_v $ and $ r_v $ .
To make Parsa's tree look even more majestic, Nima wants to assign a number $ a_v $ ( $ l_v \le a_v \le r_v $ ) to each vertex $ v $ such that the beauty of Parsa's tree is maximized.
Nima's sense of the beauty is rather bizarre. He defines the beauty of the tree as the sum of $ |a_u - a_v| $ over all edges $ (u, v) $ of the tree.
Since Parsa's tree is too large, Nima can't maximize its beauty on his own. Your task is to find the maximum possible beauty for Parsa's tree.
输入格式
The first line contains an integer $ t $ $ (1\le t\le 250) $ — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer $ n $ $ (2\le n\le 10^5) $ — the number of vertices in Parsa's tree.
The $ i $ -th of the following $ n $ lines contains two integers $ l_i $ and $ r_i $ $ (1 \le l_i \le r_i \le 10^9) $ .
Each of the next $ n-1 $ lines contains two integers $ u $ and $ v $ $ (1 \le u , v \le n, u\neq v) $ meaning that there is an edge between the vertices $ u $ and $ v $ in Parsa's tree.
It is guaranteed that the given graph is a tree.
It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^5 $ .
输出格式
For each test case print the maximum possible beauty for Parsa's tree.
样例 #1
样例输入 #1
3
2
1 6
3 8
1 2
3
1 3
4 6
7 9
1 2
2 3
6
3 14
12 20
12 19
2 12
10 17
3 17
3 2
6 5
1 5
2 6
4 6
样例输出 #1
7
8
62
提示
The trees in the example:
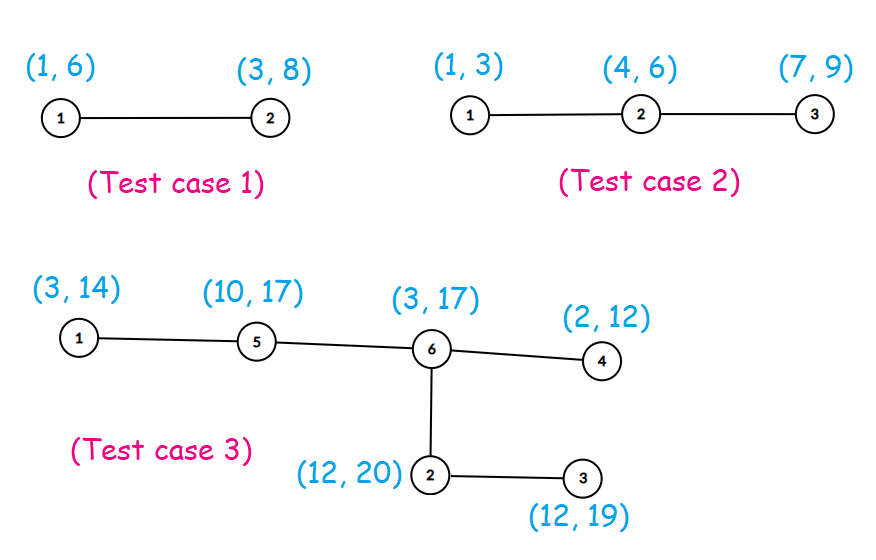
In the first test case, one possible assignment is $ a = {1, 8} $ which results in $ |1 - 8| = 7 $ .
In the second test case, one of the possible assignments is $ a = {1, 5, 9} $ which results in a beauty of $ |1 - 5| + |5 - 9| = 8 $
思路
考虑树形DP:
显然,每个点取的一定是取边界的时候最有,
状态表示:表示以为根的子树中,选左边界(0)和选右边界(1)的最大值
状态转移:
- 选左边界:
- 选右边界:
即以x为根节点,如果选了左边界,那么他的所有儿子y可以选左边界,或者右边界,两者取最大值
结果:
注意:本题不开读入优化会TLE,如果忘记清空vector建图,会MLE。
代码
#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define cxk 1
#define debug(s, x) \
if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;
const int N = 1e5 + 10;
vector<int> e[N];
int f[N][2], l[N], r[N];
void dfs(int x, int fa) {
for (auto y : e[x]) {
if (y == fa) continue;
dfs(y, x);
f[x][0] += max(f[y][0] + abs(l[x] - l[y]), f[y][1] + abs(l[x] - r[y]));
f[x][1] += max(f[y][0] + abs(r[x] - l[y]), f[y][1] + abs(r[x] - r[y]));
}
}
void solve() {
int n;
cin >> n;
for (int i = 1; i <= n; i++) e[i].clear();
for (int i = 1; i <= n; i++) f[i][1] = f[i][0] = 0;
for (int i = 1; i <= n; i++) cin >> l[i] >> r[i];
for (int i = 1; i <= n - 1; i++) {
int x, y;
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
dfs(1, 0);
int t = max(f[1][0], f[1][1]);
cout << t << endl;
}
signed main() {
cin.tie(0), cout.tie(0);
ios::sync_with_stdio(false);
int _ = 1;
cin >> _;
while (_--) solve();
return 0;
}
Add One
题面翻译
称“将一个数上每一位的值”为一次操作,例如对于进行一次操作后的结果为。输入,输出对进行次操作的结果。
题目描述
You are given an integer $ n $ . You have to apply $ m $ operations to it.
In a single operation, you must replace every digit $ d $ of the number with the decimal representation of integer $ d + 1 $ . For example, $ 1912 $ becomes $ 21023 $ after applying the operation once.
You have to find the length of $ n $ after applying $ m $ operations. Since the answer can be very large, print it modulo $ 10^9+7 $ .
输入格式
The first line contains a single integer $ t $ ( $ 1 \le t \le 2 \cdot 10^5 $ ) — the number of test cases.
The only line of each test case contains two integers $ n $ ( $ 1 \le n \le 10^9 $ ) and $ m $ ( $ 1 \le m \le 2 \cdot 10^5 $ ) — the initial number and the number of operations.
输出格式
For each test case output the length of the resulting number modulo $ 10^9+7 $ .
样例 #1
样例输入 #1
5
1912 1
5 6
999 1
88 2
12 100
样例输出 #1
5
2
6
4
2115
提示
For the first test, $ 1912 $ becomes $ 21023 $ after $ 1 $ operation which is of length $ 5 $ .
For the second test, $ 5 $ becomes $ 21 $ after $ 6 $ operations which is of length $ 2 $ .
For the third test, $ 999 $ becomes $ 101010 $ after $ 1 $ operation which is of length $ 6 $ .
For the fourth test, $ 88 $ becomes $ 1010 $ after $ 2 $ operations which is of length $ 4 $ .
思路
数位DP?
只需要一位一位的考虑每个数字,n中的数字之间是互不影响的,先进行dp预处理0-10的每个数字经过j次操作之后的位数
状态表示:表示当前的数字为,需要操作的次数为之后的长度 ()
状态转移:
- 如果,则数字还是一位 ,即
- 如果 则产生进位,可以先用个操作,使得这个数字变成,剩余的操作次数为,即
注意:需要先枚举操作次数j,再枚举i,否则可能出现没有计算的情况
读入需要优化,需要取模
代码
#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define cxk 1
#define debug(s, x) \
if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;
const int N = 2e5 + 10, mod = 1e9 + 7;
int f[10][N];
void solve() {
string s;
int m;
cin >> s >> m;
int res = 0;
for (auto c : s) {
int t = f[c - '0'][m];
res = (res + f[c - '0'][m]) % mod;
}
cout << res << endl;
}
void init() {
for (int j = 0; j < N; j++) {
for (int i = 0; i <= 9; i++) {
if (i + j < 10) {
f[i][j] = 1;
} else {
f[i][j] = (f[0][i + j - 10] + f[1][i + j - 10]) % mod;
}
}
}
}
signed main() {
cin.tie(0), cout.tie(0);
ios::sync_with_stdio(false);
init();
int _ = 1;
cin >> _;
while (_--) solve();
return 0;
}
Distinct Characters Queries
题面翻译
一个字符串s,和q个操作(包括以下两个)
- 1 pos c 将s[pos]上的字符变为c
- 2 l r 输出[l,r]中有多少个不同的字符
题目描述
You are given a string $ s $ consisting of lowercase Latin letters and $ q $ queries for this string.
Recall that the substring $ s[l; r] $ of the string $ s $ is the string $ s_l s_{l + 1} \dots s_r $ . For example, the substrings of "codeforces" are "code", "force", "f", "for", but not "coder" and "top".
There are two types of queries:
- $ 1~ pos~ c $ ( $ 1 \le pos \le |s| $ , $ c $ is lowercase Latin letter): replace $ s_{pos} $ with $ c $ (set $ s_{pos} := c $ );
- $ 2~ l~ r $ ( $ 1 \le l \le r \le |s| $ ): calculate the number of distinct characters in the substring $ s[l; r] $ .
输入格式
The first line of the input contains one string $ s $ consisting of no more than $ 10^5 $ lowercase Latin letters.
The second line of the input contains one integer $ q $ ( $ 1 \le q \le 10^5 $ ) — the number of queries.
The next $ q $ lines contain queries, one per line. Each query is given in the format described in the problem statement. It is guaranteed that there is at least one query of the second type.
输出格式
For each query of the second type print the answer for it — the number of distinct characters in the required substring in this query.
样例 #1
样例输入 #1
abacaba
5
2 1 4
1 4 b
1 5 b
2 4 6
2 1 7
样例输出 #1
3
1
2
样例 #2
样例输入 #2
dfcbbcfeeedbaea
15
1 6 e
1 4 b
2 6 14
1 7 b
1 12 c
2 6 8
2 1 6
1 7 c
1 2 f
1 10 a
2 7 9
1 10 a
1 14 b
1 1 f
2 1 11
样例输出 #2
5
2
5
2
6
思路
考虑使用STL中的set进行操作:,可以开26个set,分别存每个字母出现的下标
- 单点修改:将原来字母的set里面的下标idx删去,然后修改s中的字母,再将修改后的字母对应的set插入坐标idx
- 区间查询:由于每个字母最多在区间中出现一次,因此可以遍历26个字母,找第一个的数(即坐标),如果可以找到并且,说明这个字母在区间中出现了,对答案的贡献+1
代码
#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define cxk 1
#define debug(s, x) \
if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;
void solve() {
string s;
cin >> s;
int n = s.size();
s = " " + s;
vector<set<int>> pos(26);
for (int i = 1; i <= n; i++) {
pos[s[i] - 'a'].insert(i);
}
auto update = [&](int idx, char c) {
pos[s[idx] - 'a'].erase(idx);
s[idx] = c;
pos[c - 'a'].insert(idx);
};
auto query = [&](int l, int r) {
int res = 0;
for (int i = 0; i < 26; i++) {
auto it = pos[i].lower_bound(l);
if (it != pos[i].end() && *it <= r) res++;
}
return res;
};
int q;
cin >> q;
while (q--) {
int op;
cin >> op;
if (op == 1) {
int idx;
char c;
cin >> idx >> c;
update(idx, c);
} else {
int l, r;
cin >> l >> r;
cout << query(l, r) << endl;
}
}
}
signed main() {
int _ = 1;
while (_--) solve();
return 0;
}
Kuroni and Impossible Calculation
https://www.luogu.com.cn/problem/CF1305C
题面翻译
- 给定 个整数 和一个整数 。
- 你需要求出 的值。
- ,,。
题目描述
To become the king of Codeforces, Kuroni has to solve the following problem.
He is given $ n $ numbers $ a_1, a_2, \dots, a_n $ . Help Kuroni to calculate $ \prod_{1\le i<j\le n} |a_i - a_j| $ . As result can be very big, output it modulo $ m $ .
If you are not familiar with short notation, $ \prod_{1\le i<j\le n} |a_i - a_j| $ is equal to $ |a_1 - a_2|\cdot|a_1 - a_3|\cdot $ $ \dots $ $ \cdot|a_1 - a_n|\cdot|a_2 - a_3|\cdot|a_2 - a_4|\cdot $ $ \dots $ $ \cdot|a_2 - a_n| \cdot $ $ \dots $ $ \cdot |a_{n-1} - a_n| $ . In other words, this is the product of $ |a_i - a_j| $ for all $ 1\le i < j \le n $ .
输入格式
The first line contains two integers $ n $ , $ m $ ( $ 2\le n \le 2\cdot 10^5 $ , $ 1\le m \le 1000 $ ) — number of numbers and modulo.
The second line contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 0 \le a_i \le 10^9 $ ).
输出格式
Output the single number — $ \prod_{1\le i<j\le n} |a_i - a_j| \bmod m $ .
样例 #1
样例输入 #1
2 10
8 5
样例输出 #1
3
样例 #2
样例输入 #2
3 12
1 4 5
样例输出 #2
0
样例 #3
样例输入 #3
3 7
1 4 9
样例输出 #3
1
提示
In the first sample, $ |8 - 5| = 3 \equiv 3 \bmod 10 $ .
In the second sample, $ |1 - 4|\cdot|1 - 5|\cdot|4 - 5| = 3\cdot 4 \cdot 1 = 12 \equiv 0 \bmod 12 $ .
In the third sample, $ |1 - 4|\cdot|1 - 9|\cdot|4 - 9| = 3 \cdot 8 \cdot 5 = 120 \equiv 1 \bmod 7 $ .
思路
注意到m很小,只有1000,
当的时候,根据鸽笼原理,一定会有两个数它们的模的结果是相同的,即,则一定会存在一项,此时答案就为0
当的时候,,因此暴力算即可。
代码
#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) \
if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;
void solve() {
int n, m;
cin >> n >> m;
vector<int> a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
if (n > m) {
cout << 0 << endl;
} else {
int res = 1;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
int t = abs(a[i] - a[j]) % m;
res = (res * t) % m;
}
}
cout << res << endl;
}
}
signed main() {
IOS int _ = 1;
while (_--) solve();
return 0;
}
Obtain The String
题面翻译
给定两个字符串 和 。有一个初始为空的字符串 ,每次操作可以往 的末尾加上一个 的子序列,问至少经过多少次操作才能使 变成 ,如果不可能输出 。
题目描述
You are given two strings $ s $ and $ t $ consisting of lowercase Latin letters. Also you have a string $ z $ which is initially empty. You want string $ z $ to be equal to string $ t $ . You can perform the following operation to achieve this: append any subsequence of $ s $ at the end of string $ z $ . A subsequence is a sequence that can be derived from the given sequence by deleting zero or more elements without changing the order of the remaining elements. For example, if $ z = ac $ , $ s = abcde $ , you may turn $ z $ into following strings in one operation:
- $ z = acace $ (if we choose subsequence $ ace $ );
- $ z = acbcd $ (if we choose subsequence $ bcd $ );
- $ z = acbce $ (if we choose subsequence $ bce $ ).
Note that after this operation string $ s $ doesn't change.
Calculate the minimum number of such operations to turn string $ z $ into string $ t $ .
输入格式
The first line contains the integer $ T $ ( $ 1 \le T \le 100 $ ) — the number of test cases.
The first line of each testcase contains one string $ s $ ( $ 1 \le |s| \le 10^5 $ ) consisting of lowercase Latin letters.
The second line of each testcase contains one string $ t $ ( $ 1 \le |t| \le 10^5 $ ) consisting of lowercase Latin letters.
It is guaranteed that the total length of all strings $ s $ and $ t $ in the input does not exceed $ 2 \cdot 10^5 $ .
输出格式
For each testcase, print one integer — the minimum number of operations to turn string $ z $ into string $ t $ . If it's impossible print $ -1 $ .
样例 #1
样例输入 #1
3
aabce
ace
abacaba
aax
ty
yyt
样例输出 #1
1
-1
3
思路
遇到这种字符串的问题,可以不用去想位置上面是哪个数,而考虑哪个数出现在哪些位置。
显然本题如果没有t里面的字符就是无解,否则一定有解。
记录上一个字符出现的位置为last
那考虑当前字符的时候,只需要在对应的pos数组里面去二分找>last的最小位置即可,如果找不到,答案就加1,并且last设置为当前数组的第一个坐标。
代码
#include <bits/stdc++.h>
#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;
void solve() {
string s, t;
cin >> s >> t;
vector<int> pos[200];
for (int i = 0; i < s.size(); ++i) pos[s[i]].push_back(i);
int last = -1;
int res = 1;
for (int i = 0; i < t.size(); ++i) {
char c = t[i];
if (pos[c].empty()) {
cout << -1 << endl;
return;
}
int idx = std::upper_bound(pos[c].begin(), pos[c].end(), last) - pos[c].begin();
if (idx == pos[c].size()) {
res++;
last = pos[c].front();
} else {
last = pos[c][idx];
}
}
cout << res << endl;
}
signed main() {
IOS
#ifndef ONLINE_JUDGE
freopen("../test.in", "r", stdin);
freopen("../test.out", "w", stdout);
#endif
int _ = 1;
cin >> _;
while (_--) solve();
return 0;
}
