移棋子游戏

题目

https://vjudge.csgrandeur.cn/problem/LibreOJ-10243

给定一个有 N 个节点的有向无环图，图中某些节点上有棋子，两名玩家交替移动棋子。

玩家每一步可将任意一颗棋子沿一条有向边移动到另一个点，无法移动者输掉游戏。

对于给定的图和棋子初始位置，双方都会采取最优的行动，询问先手必胜还是先手必败。

输入格式

第一行，三个整数 N , M, K ， N 表示图中节点总数， M 表示图中边的条数， K 表示棋子的个数。

接下来 M 行，每行两个整数 X, Y 表示有一条边从 X 出发指向 Y 。

接下来一行， K 个空格间隔的整数，表示初始时，棋子所在的节点编号。

输出格式

若先手胜，输出 win，否则输出 lose。

输入样例

6 8 4
2 1
2 4
1 4
1 5
4 5
1 3
3 5
3 6
1 2 4 6

输出样例

win

数据范围与提示

对于全部数据，$N \le 2000, M \le 6000, 1 \le K \le N$。

思路

$mex$运算：$mes(S)=min\{x\}(x\in N,x \notin S)$，即x为不属于集合S的最小非负整数

SG函数：设状态$x$有$k$个后继状态$y_1,y_2...y_k$,则$SG(x)=mex(\{ SG(y_1),SG(y_2)...SG(y_k) \})$

SG定理：由n个有向图游戏组成的组合游戏，设起点分别为$s_1,s_2...s_n$，当$SG(s1) \land SG(s2)... \land SG(s_n)!=0$

时，先手必胜，否则，先手必败

SG图如下：

image-20230719152736972

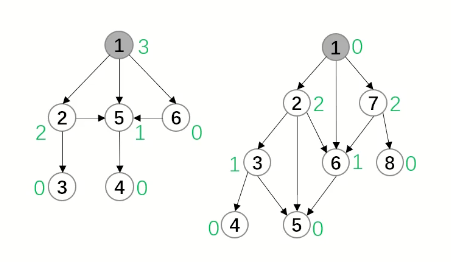
在本题中，每个棋子都是孤立的，k个棋子可以拆分成k个有向图游戏，利用SG定理判断即可。

image-20230719152906253

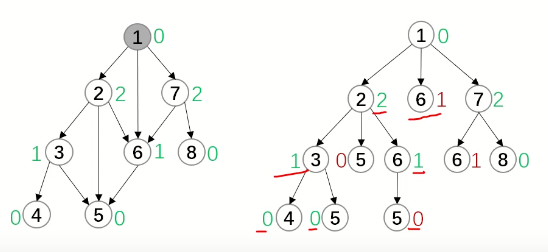
代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 2e3 + 10;

vector<int> e[N];
int f[N];

int dfs(int x) {
    if (f[x] != -1) return f[x];
    set<int> s;
    for (auto y: e[x]) {
        s.insert(dfs(y));
    }
    for (int i = 0;; i++) {
        if (!s.count(i)) return f[x] = i;
    }

}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int n, m, k;
    cin >> n >> m >> k;
    for (int i = 1; i <= m; i++) {
        int x, y;
        cin >> x >> y;
        e[x].push_back(y);
    }
    memset(f, -1, sizeof f);
    int res = 0;
    while (k--) {
        int x;
        cin >> x;
        res ^= dfs(x);
    }
    if (res) cout << "win"; else cout << "lose";


    return 0;
}

集合-Nim游戏

题目

https://www.acwing.com/problem/content/895/

给定 $n$ 堆石子以及一个由 $k$ 个不同正整数构成的数字集合 $S$。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 $S$，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式

第一行包含整数 $k$，表示数字集合 $S$ 中数字的个数。

第二行包含 $k$ 个整数，其中第 $i$ 个整数表示数字集合 $S$ 中的第 $i$ 个数 $s_i$。

第三行包含整数 $n$。

第四行包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 堆石子的数量 $h_i$。

输出格式

如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围

$1 \le n, k \le 100$,
$1 \le s_i,h_i \le 10000$

输入样例：

2
2 5
3
2 4 7

输出样例：

Yes

思路

和上一题类似，这里当前点x可以到达的状态为$x-a[i](x-a[i]>=0)$,

因此记忆化搜索的时候搜这些点

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 110,M=10010;
int a[N];
int n, k, h[M];
int f[M];

int dfs(int x) {
    if (f[x] != -1) return f[x];
    set<int> s;
    for (int i = 1; i <= k; i++) {
        if (x - a[i] >= 0) s.insert(dfs(x - a[i]));
    }
    for (int i = 0;; i++) {
        if (!s.count(i)) return f[x] = i;
    }
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    cin >> k;
    for (int i = 1; i <= k; i++) cin >> a[i];
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> h[i];
    memset(f, -1, sizeof f);
    int res = 0;
    for (int i = 1; i <= n; i++) {
        res ^= dfs(h[i]);
    }
    if (res) cout << "Yes";
    else cout << "No";


    return 0;
}

剪纸游戏

题目

https://www.acwing.com/problem/content/221/

给定一张 $N \times M$ 的矩形网格纸，两名玩家轮流行动。

在每一次行动中，可以任选一张矩形网格纸，沿着某一行或某一列的格线，把它剪成两部分。

首先剪出 $1 \times 1$ 的格纸的玩家获胜。

两名玩家都采取最优策略行动，求先手是否能获胜。

提示：开始时只有一张纸可以进行裁剪，随着游戏进行，纸张被裁剪成 $2,3,…$ 更多张，可选择进行裁剪的纸张就会越来越多。

输入格式

输入包含多组测试数据，每组数据占一行。

每组数据包括两个整数 $N$ 和 $M$，表示初始网格纸的尺寸。

输出格式

每组测试数据输出一个结果，结果占一行。

如果先手方必胜，则输出 WIN；

如果先手方必输，则输出 LOSE。

数据范围

$2 \le N,M \le 200$

输入样例：

2 2
3 2
4 2

输出样例：

LOSE
LOSE
WIN

思路

因为最后的1*1是一个必胜态，但是我们平时做的sg函数的结果异或和为0得到的是一个必败态。因此可以先把本题转化为必败态来做：

image-20230719164153987

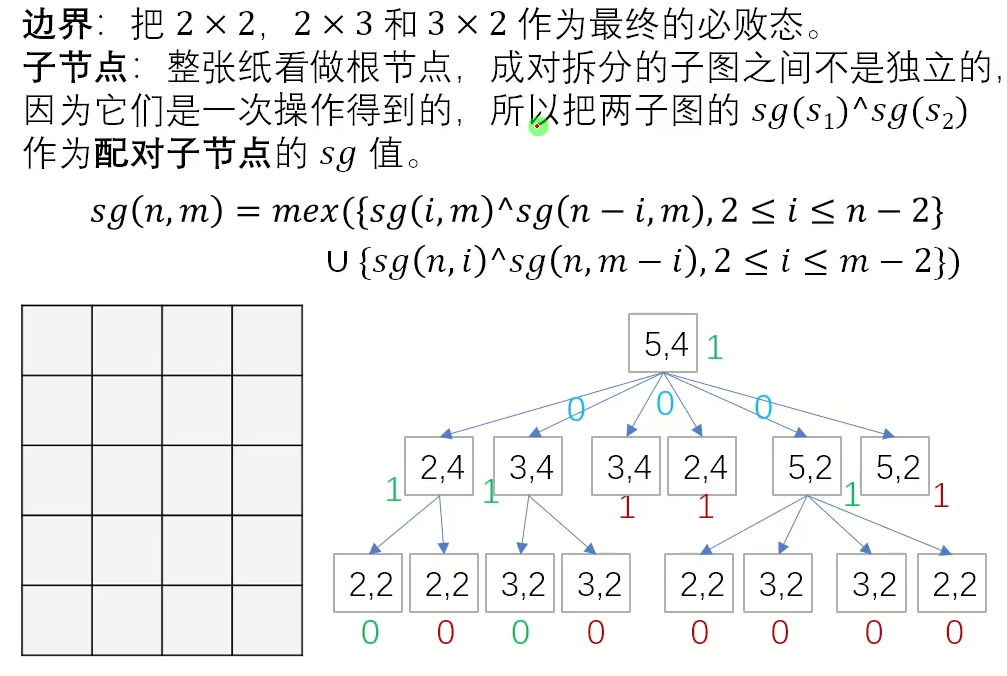
代码

#include <bits/stdc++.h>

#define int long long
using namespace std;

const int N = 210;
int n, m;
int f[N][N];

int dfs(int a, int b) {
    if (f[a][b] != -1) return f[a][b];
    set<int> s;
    for (int i = 2; i <= a - 2; i++) {
        s.insert(dfs(i, b) ^ dfs(a - i, b));
    }

    for (int i = 2; i <= b - 2; i++) {
        s.insert(dfs(a, i) ^ dfs(a, b - i));
    }
    for (int i = 0;; i++) {
        if (!s.count(i)) return f[a][b] = f[b][a] = i;
    }
}


signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    memset(f, -1, sizeof f);
    while (cin >> n >> m) cout << (dfs(n, m) ? "WIN" : "LOSE") << endl;

    return 0;
}