计算几何

点线关系

点的结构体如下：

struct Point {
    double x, y;
};

点积

定义：$\vec{a}*\vec{b}=|a|*|b|*cos(\theta)$

几何意义：向量b在向量a上的投影与向量a的长度的乘积

坐标运算：$\vec{a}*\vec{b}=x_1x_2+y_1y_2$

应用

1. 两向量垂直:$\vec{a}*\vec{b}=0$
2. 两向量平行：$\vec{a}*\vec{b}=|a|*|b|$
3. 两向量夹角：$cos(\theta)=\frac{\vec{a}\vec{b}}{|a||b|}$

image-20230822184201417

叉积

定义：$\vec{a}*\vec{b}=|a|*|b|*si n(\theta)$

几何意义：两个向量形成的平行四边形的面积，b在a逆时针方向为正

运算：$\vec{a}*\vec{b}=x_1y_2-y_1x_2$

应用：判断点线位置关系：

image-20230822184217460

代码模版

struct Point {
    double x, y;

    Point operator+(Point b) const {
        return {x + b.x, y + b.y};
    }

    Point operator-(Point b) const {
        return {x - b.x, y - b.y};
    }

    double operator*(Point b) const { //点积
        return x * b.x + y * b.y;
    }
  
    Point operator*(int t) const {
        return {x * t, y * t};
    }

    double operator&(Point b) const {//叉积
        return x * b.y - y * b.x;
    }
};


double len(Point a) { //模
    return sqrt(a.x * a.x + a.y * a.y);
}

double angle(Point a, Point b) { //cos夹角
    double t = a * b / len(a) / len(b);
    return acos(t);
}

double cross(Point a, Point b, Point c) { //两个向量叉积
    return (c - a) & (b - a);//>0 c在ab左侧 =0 共线
}

double dis(Point a, Point b) {
    double t = (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
    return sqrt(t);
}

线线关系

image-20230822194352884

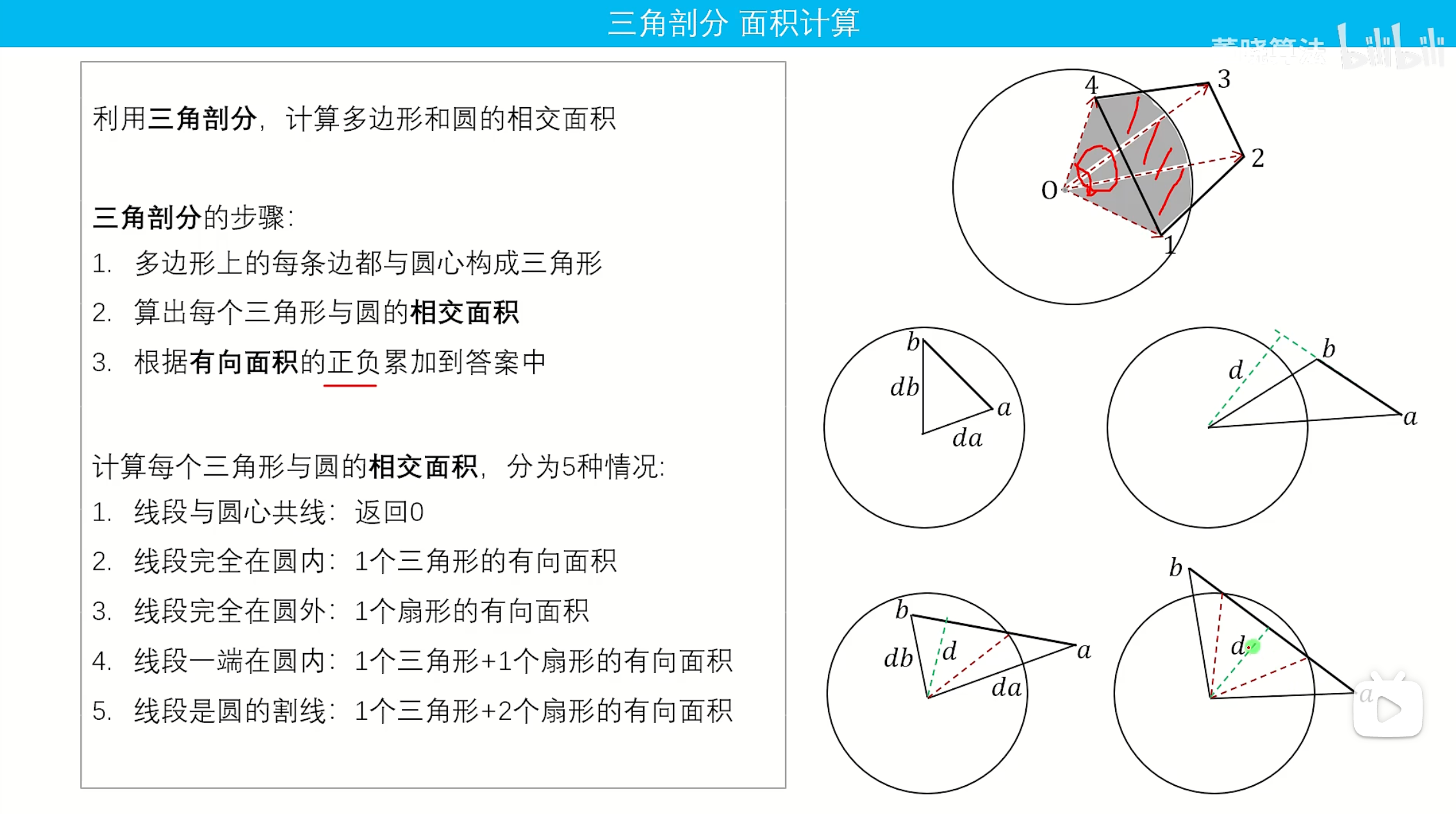
三角剖分

image-20230822201323976