LeetCode第101场双周赛
6327. 从两个数字数组里生成最小数字
题目
给你两个只包含 1 到 9 之间数字的数组 nums1 和 nums2 ,每个数组中的元素 互不相同 ,请你返回 最小 的数字,两个数组都 至少 包含这个数字的某个数位。
示例 1:
输入:nums1 = [4,1,3], nums2 = [5,7]
输出:15
解释:数字 15 的数位 1 在 nums1 中出现,数位 5 在 nums2 中出现。15 是我们能得到的最小数字。
示例 2:
输入:nums1 = [3,5,2,6], nums2 = [3,1,7]
输出:3
解释:数字 3 的数位 3 在两个数组中都出现了。
提示:
1 <= nums1.length, nums2.length <= 9
1 <= nums1[i], nums2[i] <= 9
每个数组中,元素 互不相同 。
思路
可以先用一个map记录是否有相同的数字出现,因为map是自动排序的,如果遍历map遇到第一个出现两次的数字,那么说明这个数字就是可以获得的最小值,如果没有同时出现的,那么就分别找两个数组中的最小值a,b如果a>b,则交换,最小值=10*a+b;
代码
class Solution {
public:
int minNumber(vector<int>& nums1, vector<int>& nums2) {
int min1=10,min2=10;
map<int,int> m;
for(int x:nums1) {
min1=min(x,min1);
m[x]++;
}
for(int x:nums2) {
min2=min(x,min2);
m[x]++;
}
for(auto x:m){
if(x.second==2){
return x.first;
}
}
if(min1>min2) swap(min1,min2);
if(min2==0) return 0;
else{
int res=min2+min1*10;
return res;
}
}
};
6328. 找到最大开销的子字符串
题目
给你一个字符串 s ,一个字符 互不相同 的字符串 chars 和一个长度与 chars 相同的整数数组 vals 。
子字符串的开销 是一个子字符串中所有字符对应价值之和。空字符串的开销是 0 。
字符的价值 定义如下:
如果字符不在字符串 chars 中,那么它的价值是它在字母表中的位置(下标从 1 开始)。 比方说,'a' 的价值为 1 ,'b' 的价值为 2 ,以此类推,'z' 的价值为 26 。 否则,如果这个字符在 chars 中的位置为 i ,那么它的价值就是 vals[i] 。 请你返回字符串 s 的所有子字符串中的最大开销。
示例 1:
输入:s = "adaa", chars = "d", vals = [-1000] 输出:2 解释:字符 "a" 和 "d" 的价值分别为 1 和 -1000 。 最大开销子字符串是 "aa" ,它的开销为 1 + 1 = 2 。 2 是最大开销。 示例 2:
输入:s = "abc", chars = "abc", vals = [-1,-1,-1] 输出:0 解释:字符 "a" ,"b" 和 "c" 的价值分别为 -1 ,-1 和 -1 。 最大开销子字符串是 "" ,它的开销为 0 。 0 是最大开销。
提示:
s 只包含小写英文字母。 1 <= chars.length <= 26 chars 只包含小写英文字母,且 互不相同 。 vals.length == chars.length -1000 <= vals[i] <= 1000
思路
可以先用一个哈希表记录每个a-z的字符的值,再去将chars的值记录在这个哈希表中。
然后遍历这个字符串s,用sum表示当前这个字段的总和,如果发现<0了,那么则更新sum为了,否则继续往前加。
或者用动态规划的思想:
定义f[i]表示以a[i]结尾的最大子字符串之和,状态转移如下:
- 如果
a[i]接前面的,则f[i]=f[i-1]+a[i] - 如果
a[i]不接前面的,则f[i]=a[i]
状态转移方程为:f[i]=max(f[i],0)+a[i]
代码
class Solution {
public:
int maximumCostSubstring(string s, string chars, vector<int>& vals) {
map<char,int> m;
for(int i=1;i<=26;i++){
m[char('a'+i-1)]=i;
}
for(int i=0;i<chars.size();i++){
m[chars[i]]=vals[i];
}
int res=0,sum=0;
for(int i=0;i<s.size();i++){
sum+=m[s[i]];
if(sum<0) sum=0;
res=max(res,sum);
}
return res;
}
};
6330. 图中的最短环
现有一个含 n 个顶点的 双向 图,每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示,其中 edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接,并且不存在与自身相连的顶点。
返回图中 最短 环的长度。如果不存在环,则返回 -1 。
环 是指以同一节点开始和结束,并且路径中的每条边仅使用一次。
示例 1:
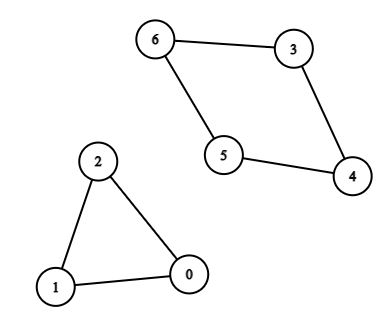
输入:n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]]
输出:3
解释:长度最小的循环是:0 -> 1 -> 2 -> 0
示例 2:
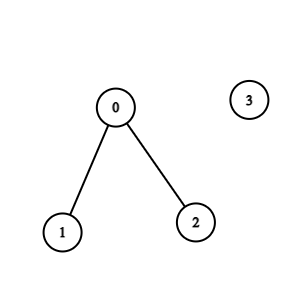
输入:n = 4, edges = [[0,1],[0,2]]
输出:-1
解释:图中不存在循环
提示:
2 <= n <= 1000 1 <= edges.length <= 1000 edges[i].length == 2 0 <= ui, vi < n ui != vi 不存在重复的边
思路
BFS求最小环:
对于每个点,做一遍BFS,如果在BFS的过程中发现某个点的相连的点已经被访问过了,说明找到了一个最小环,更新答案。
代码
class Solution {
public:
int findShortestCycle(int n, vector<vector<int>>& edges) {
int res=-1;
vector<int> g[n];
for(const auto &edge:edges){
int x=edge[0],y=edge[1];
g[x].push_back(y);
g[y].push_back(x);
}
for(int i=0;i<n;i++){
vector<int> dist(n,-1);
vector<int> pre(n,-1);
queue<int> q;
q.push(i);
dist[i]=0;
while(q.size()){
auto x=q.front();
q.pop();
for(const auto &y:g[x]){
if(dist[y]==-1){
dist[y]=dist[x]+1;
pre[y]=x;
q.push(y);
}else{
if(pre[x]!=y){
int len=dist[x]+dist[y]+1;
if(res==-1) res=len;
else res=min(res,len);
}
}
}
}
}
return res;
}
};
