2024.04.30小米暑期一面

1.自我介绍

2. Java的基本数据类型

Java 中有 8 种基本数据类型，分别为：

• 6 种数字类型：
  • 4 种整数型：byte、short、int、long
  • 2 种浮点型：float、double
• 1 种字符类型：char
• 1 种布尔型：boolean。

3.了解哪些基本的数据结构

数组、链表、栈、队列、树、图

4.简单介绍二叉树

二叉树由一个根节点和两个子树(左子树和右子树)组成。每个节点最多只能有两个孩子节点,即左子节点和右子节点。

5.知道MySQL吗？MySQL中跟二叉树相关的结构你知道吗？

参考链接

MySQL是数据库。

MySQL中跟二叉树有关的结构是B+树索引。B+树是通过二叉查找树，再由 平衡二叉树，B 树演化而来。

• 二分查找树：二分查找树虽然是一个天然的二分结构，能很好的利用二分查找快速定位数据，但是它存在一种极端的情况，每当插入的元素都是树内最大的元素，就会导致二分查找树退化成一个链表，此时查询复杂度就会从 O(logn)降低为 O(n)。
• 平衡树：为了解决二分查找树的问题，使用自平衡二叉树，保证了查询操作的时间复杂度就会一直维持在 O(logn) 。但是它本质上还是一个二叉树，每个节点只能有 2 个子节点，随着元素的增多，树的高度会越来越高。
• B树：树的高度决定于磁盘 I/O 操作的次数，为了解决这个问题，可以使用B树。它不再限制一个节点就只能有 2 个子节点，而是允许 M 个子节点 (M>2)，从而降低树的高度。 B 树的每个节点都包含数据（索引+记录），而用户的记录数据的大小很有可能远远超过了索引数据，这就需要花费更多的磁盘 I/O 操作次数来读到「有用的索引数据」。
• B+树：B+ 树就是对 B 树做了一个升级，
  • 叶子节点（最底部的节点）才会存放实际数据（索引+记录），非叶子节点只会存放索引；
  • 所有索引都会在叶子节点出现，叶子节点之间构成一个有序链表；
  • 非叶子节点的索引也会同时存在在子节点中，并且是在子节点中所有索引的最大（或最小）。
  • 非叶子节点中有多少个子节点，就有多少个索引；

6.展开说说B树和B+树

参考链接

B 树也称 B-树,全称为 多路平衡查找树 ，B+ 树是 B 树的一种变体。B 树和 B+树中的 B 是 Balanced （平衡）的意思。

目前大部分数据库系统及文件系统都采用 B-Tree 或其变种 B+Tree 作为索引结构。

B 树& B+树两者有何异同呢？

• B 树的所有节点既存放键(key) 也存放数据(data)，而 B+树只有叶子节点存放 key 和 data，其他内节点只存放 key。
• B 树的叶子节点都是独立的;B+树的叶子节点有一条引用链指向与它相邻的叶子节点。
• B 树的检索的过程相当于对范围内的每个节点的关键字做二分查找，可能还没有到达叶子节点，检索就结束了。而 B+树的检索效率就很稳定了，任何查找都是从根节点到叶子节点的过程，叶子节点的顺序检索很明显。
• 在 B 树中进行范围查询时，首先找到要查找的下限，然后对 B 树进行中序遍历，直到找到查找的上限；而 B+树的范围查询，只需要对链表进行遍历即可。

综上，B+树与 B 树相比，具备更少的 IO 次数、更稳定的查询效率和更适于范围查询这些优势。

8.Redis的基本类型

String、List、Hash、Set、Zset、BitMap、HyperLogLog、GEO、Stream

9.Redis中Set和Sorted Set的区别

1. 数据结构:

   • Set 是无序集合,底层使用 hash table 实现。
   • Sorted Set 是有序集合,底层使用 skiplist 和 hash table 实现。

2. 元素的值:

   • Set 中的元素是无序的,且元素的值是唯一的。
   • Sorted Set 中的每个元素都会关联一个double类型的分数(score),通过分数进行排序。元素的值也是唯一的。

3. 操作:

   • Set 支持 add、remove、contains 等基本操作。还支持交集、并集、差集等集合操作。
   • Sorted Set 除了 Set 的基本操作,还支持按照分数进行排序、范围查询等操作。

4. 应用场景:

   • Set 适合用于数据去重、标签记录等场景。
   • Sorted Set 适合用于排行榜、延时任务队列等需要按照分数排序的场景。

10.有了解过JVM方面的知识吗？垃圾回收

Java 虚拟机会自动执行内存管理,开发者不需要手动分配和释放内存。垃圾收集器会定期扫描堆内存,识别哪些对象已经不再被引用,并将其从内存中清除。

常见的垃圾回收算法：

1. 引用计数算法(Reference Counting)，给对象添加一个引用计数器,每当有一个地方引用它时,计数器就加1,引用失效时计数器减1。当对象的引用计数为0时,就可以将其回收。优点是实现简单,判断方便。缺点是无法解决循环引用的问题。

2. 可达性分析算法(Reachability Analysis)：通过一系列的"GC Roots"对象作为起点,从这些节点开始向下搜索,能搜索到的对象都是存活的,搜索不到的就是要回收的垃圾。GC Roots包括虚拟机栈、本地方法栈、方法区中的常量、静态变量等。可达性分析是目前主流的垃圾收集算法,被Java、C#等主流语言所采用。

3. 复制算法(Copying)：将内存划分为等大小的两块,每次只使用其中一块。当这一块用完时,将存活的对象复制到另一块上,然后清除掉这一块内存。优点是实现简单,没有内存碎片问题。缺点是内存利用率低,只有50%。

4. 标记-清除算法(Mark-Sweep)：分为标记和清除两个阶段,先标记出所有需要回收的对象,然后统一回收这些对象。优点是不需要额外的空间存储，充分利用了现有空间。缺点是需要扫描整个堆内存,效率较低,且会产生内存碎片。

5. 标记-整理算法(Mark-Compact)：在标记-清除算法的基础上,将存活对象移动到内存的一端,将碎片化的内存整理到一起。解决了标记-清除算法产生内存碎片的问题。

11.TCP通过什么来保证可靠传输的？

TCP 是通过序列号、确认应答、重发控制、连接管理以及窗口控制等机制实现可靠性传输的。

12.细说三次握手、四次挥手

参考链接

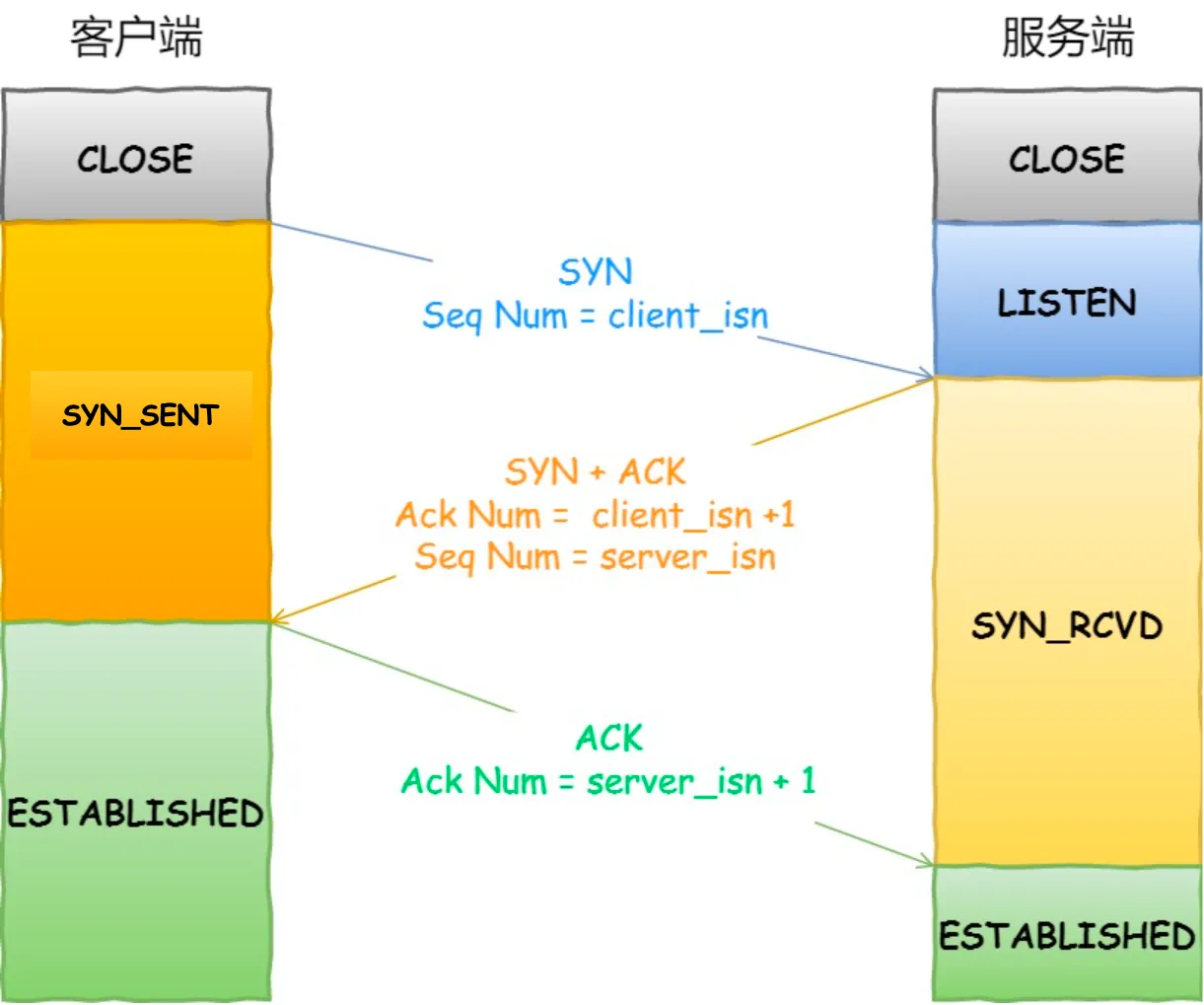
• 一开始，客户端和服务端都处于 CLOSE 状态。先是服务端主动监听某个端口，处于 LISTEN 状态
• 客户端会随机初始化序号（client_isn），将此序号置于 TCP 首部的「序号」字段中，同时把 SYN(同步序列编号) 标志位置为 1，表示 SYN 报文。接着把第一个 SYN 报文发送给服务端，表示向服务端发起连接，该报文不包含应用层数据，之后客户端处于 SYN-SENT 状态。
• 服务端收到客户端的 SYN 报文后，首先服务端也随机初始化自己的序号（server_isn），将此序号填入 TCP 首部的「序号」字段中，其次把 TCP 首部的「确认应答号」字段填入 client_isn + 1, 接着把 SYN 和 ACK(确认编号) 标志位置为 1。最后把该报文发给客户端，该报文也不包含应用层数据，之后服务端处于 SYN-RCVD 状态。
• 客户端收到服务端报文后，还要向服务端回应最后一个应答报文，首先该应答报文 TCP 首部 ACK 标志位置为 1 ，其次「确认应答号」字段填入 server_isn + 1 ，最后把报文发送给服务端，这次报文可以携带客户到服务端的数据，之后客户端处于 ESTABLISHED 状态。服务端收到客户端的应答报文后，也进入 ESTABLISHED 状态。

四次挥手：

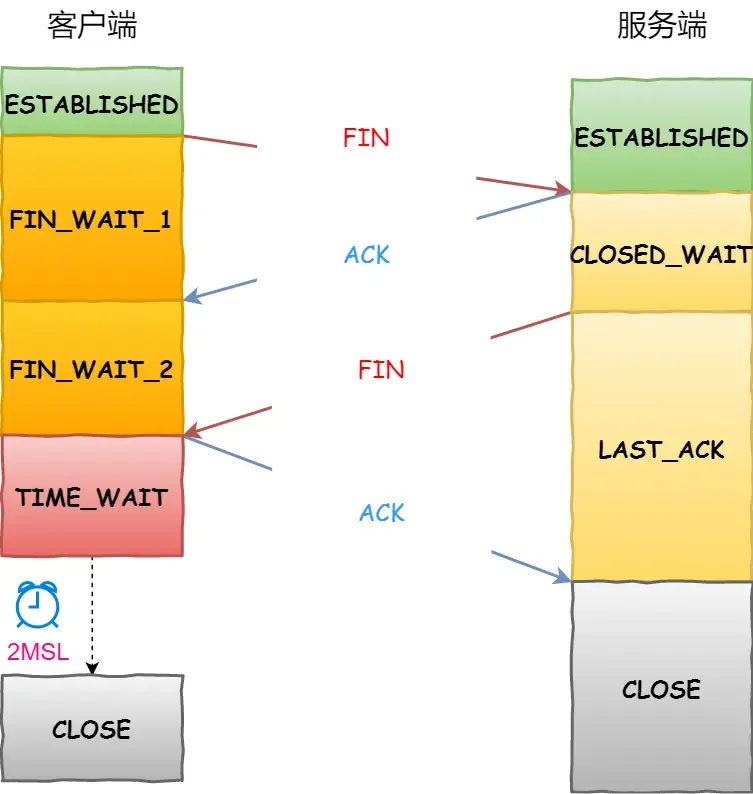
1. 第一步（FIN=1）：

• • 客户端发送一个 FIN 报文段给服务器，表示客户端已经完成数据传输，希望关闭连接。

1. 第二步（ACK=1，ACKnum=X+1）：

• • 服务器收到客户端的 FIN 报文段后，发送一个 ACK 报文段作为响应，确认收到了客户端的 FIN 报文段，并告知客户端自己也准备关闭连接。此时，服务器进入了 CLOSE_WAIT 状态。

1. 第三步（FIN=1）：

• • 服务器发送一个 FIN 报文段给客户端，表示服务器已经完成数据传输，希望关闭连接。

1. 第四步（ACK=1，ACKnum=Y+1）：

• • 客户端收到服务器的 FIN 报文段后，发送一个 ACK 报文段作为响应，确认收到了服务器的 FIN 报文段，并告知服务器自己也准备关闭连接。此时，客户端进入了 TIME_WAIT 状态。

在四次挥手过程中，最后一次的 ACK 报文段是为了确保对方收到了自己的 FIN 报文段。在正常情况下，客户端发送完 ACK 后会进入 TIME_WAIT 状态，在这个状态下会等待一段时间（通常是 2 倍的 MSL，最长为 2*MSL），然后才会关闭连接。这个等待时间是为了保证被动关闭方收到最后一个 ACK 报文段，同时防止之前的重复报文段在网络中被延迟，导致对方重新发送 FIN 报文段，产生错误。

13.链表相关，大概是将链表转成数字，相加之后再转成链表。

输入：链表一：1->6->3，链表二：7->1->2，相当于361+217=578 输出：8->7->5 需要自己定义链表结构，自己输入测试用例。

445. 两数相加 II

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverse(ListNode* l1){
        ListNode* pre=nullptr;
        ListNode* cur=l1;
        while(cur){
            ListNode *next=cur->next;
            cur->next=pre;
            pre=cur;
            cur=next;
        }
        return pre;
    }

    ListNode* add(ListNode* l1,ListNode* l2){
        ListNode* dummy=new ListNode(0);
        ListNode* cur=dummy;
        int t=0;
        while(l1||l2||t){
            if(l1) t+=l1->val;
            if(l2) t+=l2->val;
            cur->next=new ListNode(t%10);
            cur=cur->next;
            t/=10;
            if(l1)l1=l1->next;
            if(l2)l2=l2->next;
        }
        return dummy->next;
    }

    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1=reverse(l1);
        l2=reverse(l2);
        ListNode* l3=add(l1,l2);
        return reverse(l3);
    }
};