跳至主要內容

Codeforces Round 891 (Div. 3)

AlgorithmCodeforcesAlgorithmCodeforcesdiv3大约 12 分钟约 3571 字全民制作人ikun

Codeforces Round 891 (Div. 3)open in new window

A. Array Coloring

题目

给你一个由nn个整数组成的数组。您的任务是确定是否可以将其所有元素着色为两种颜色，使得两种颜色的元素之和具有相同的奇偶性，并且每种颜色至少有一个元素着色。

例如，如果数组为[1,2,4,3,2,3,5,41,2,4,3,2,3,5,4]，我们可以将其着色为：[1,2,4,3,2,3,5,4\color{blue}{1},\color{blue}{2},\color{red}{4},\color{blue}{3},\color{red}{2},\color{red}{3},\color{red}{5},\color{red}{4}]，其中蓝色元素的总和为66，红色元素的总和为【 1818。

思路

如果数组总和为奇数，那么显然分成的两组中必定有一组为奇数，另一组为偶数， 因为如果两组都是偶数或者奇数，那么总和一定是偶数。

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) cin >> a[i];
    int sum = 0;
    for (int i = 1; i <= n; i++) sum += a[i];
    if (sum % 2 == 0) yes else no

}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

B. Maximum Rounding

题目

给定一个自然数xx。您可以执行以下操作：

  • 选择一个正整数kk并将xx舍入到第kk位数字

请注意，位置从右到左编号，从零开始。如果数字有kk位，则认为第kk位的数字等于00。

舍入按如下方式完成：

  • 若第(k−1)(k-1)位的数字大于或等于55，则第kk位的数字增加11，否则为kk位的数字-th 位置保持不变（使用数学舍入）。

  • 如果运算前第kk位的数字是99，应该增加11，那么我们就查找最小的位置k′k'（k′>kk'>k），其中的数字第k′k'位的数字小于99，在第k′k'位的数字上加11。然后我们分配k=k′k=k'。

  • 之后，位置小于kk的所有数字都被替换为零。

如果您可以根据需要多次执行该操作，您的任务就是使xx尽可能大。

例如xx等于34513451，那么如果连续选择：

-k=1k=1，那么操作后xx将变成34503450
-k=2k=2，则操作后xx将变成35003500
-k=3k=3，那么操作后xx将变成40004000
-k=4k=4，那么操作后xx将变成00

为了使答案最大化，您需要先选择k=2k=2，然后选择k=3k=3，那么数字就会变成40004000。

思路

从左往右找第一个大于等于5的数，显然从这里可以开始往前进位是最优的，这时前面的数只要满足>=4就可以继续进位，因为5可以给它带来1，一直模拟直到不可以继续进位。

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

void solve() {
    string x;
    cin >> x;
    int n = x.size();
    x = "0" + x;
    for (int i = 1; i <= n; i++) {
        if (x[i] >= '5') {
            int j = i - 1;
            while (j >= 0 && x[j] >= '4') j--;
            x[j]++;
            for (j = j+1; j <= n; j++) x[j] = '0';
            if (x[0] != '0') cout << x[0];
            for (j = 1; j <= n; j++) cout << x[j];
            cout << endl;
            return;
        }
    }
    for (int i = 1; i <= n; i++) {
        cout << x[i];
    }
    cout << endl;


}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

C. Assembly via Minimums

题目

Sasha 有一个包含nn个整数的数组aa。他觉得无聊，对于ii、jj（i<ji < j），他写下了aia_i和aja_j的最小值。他获得了一个新的数组bb，大小为n⋅(n−1)2\frac{n\cdot (n-1)}{2}。

例如，如果a=a=[2,3,5,12,3,5,1]，他会写[min⁡(2,3),min⁡(2,5),min⁡(2,1),min⁡(3,5),min⁡(3,1),min(5,1)\min(2, 3), \min(2, 5), \min(2, 1), \min(3, 5), \min(3, 1), min(5, 1)]==[2,2,1,3,1,12, 2, 1, 3, 1, 1]。

然后，他将数组bb的所有元素随机洗牌。

不幸的是，他忘记了数组aa，而你的任务是恢复任何可能获得数组bb的数组aa。

数组aa的元素应在[−109,109][-10^9,10^9]范围内。

思路

可以先开一个map来记录每个数字出现的次数

显然最小值一定会在b数组中出现n-1次，接下来是第2小的数一定会在b中出现n-2次，一直模拟下去即可。最后需要加一个比数组中最大的数还要大的数，因为这个数不会出现在b中，只要>=max(b[i])就行。

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

void solve() {
    int n;
    cin >> n;
    int m = n * (n - 1) / 2;
    vector<int> a(n + 1), b(m + 1);
    for (int i = 1; i <= m; i++) cin >> b[i];
    map<int, int> mp;
    for (int i = 1; i <= m; i++) {
        mp[b[i]]++;
    }
    vector<int> res;
    int t = n - 1;
    for (auto [x, y]: mp) {
        while (y > 0) {
            y -= t;
            t--;
            res.push_back(x);
        }
    }
    res.push_back(res.back());
    for (auto i: res) cout << i << " ";
    cout << endl;
}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

D. Strong Vertices

题目

给定两个数组aa和bb，长度均为nn。两个数组的元素索引从11到nn。您正在构建一个有向图，如果au−av≥bu−bva_u-a_v \ge b_u-b_v，则存在从uu到vv（u≠vu\neq v）的边。

如果存在从VV到所有其他顶点的路径，则顶点VV被称为强顶点。

有向图中的路径是由若干个顶点组成的链，通过边连接，从顶点uu出发，沿着边的方向，可以到达顶点vv。

你的任务是找到所有强顶点。

例如，如果a=[3,1,2,4]a=[3,1,2,4]和b=[4,3,2,1]b=[4,3,2,1]，图表将如下所示：

121
121

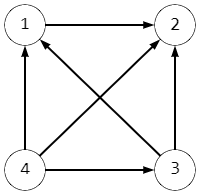
该图只有一个强顶点，编号为44

思路

转换一下题目意思就容易了：

au−av>=bu−bva_u-a_v>=b_u-b_v可以变为：au−bu>=av−bva_u-b_u>=a_v-b_v,

也就是满足题意的点一定需要满足对于其他所有顶点来说，它的a[i]−b[i]a[i]-b[i]一定要大于其他的点，即最大值因此本题只需要统计a[i]−b[i]a[i]-b[i]的最大值的数有多少个即可。

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1), b(n + 1), c(n + 1);
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> b[i], c[i] = a[i] - b[i];
    int t = *std::max_element(c.begin() + 1, c.end());
    vector<int> res;
    for (int i = 1; i <= n; i++) if (c[i] == t) res.push_back(i);
    cout << res.size() << endl;
    for (int i = 0; i < res.size(); i++) cout << res[i] << " \n"[i == res.size() - 1];
}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

E. Power of Points

题目

给你nn个带有整数坐标x1,…xnx_1,\dots x_n的点，它们位于数轴上。

对于某个整数ss，我们构造线段[s,x1s,x_1]、[s,x2s,x_2]、…\dots、[s,xns,x_n]。请注意，如果是xi<sx_i<s，那么该段将看起来像[xi,sx_i,s]。线段[a,ba, b]覆盖了所有整数点a,a+1,a+2,…,ba, a+1, a+2, \dots, b。

我们将点pp的幂定义为与坐标pp的点相交的线段数，记为fpf_p。

你的任务是计算每个s∈{x1,…,xn}s \in \{x_1,\dots,x_n\}的∑p=1109fp\sum\limits_{p=1}^{10^9}f_p，即11到10910^9所有整数点的fpf_p之和。

例如，如果初始坐标为[1,2,5,7,1][1,2,5,7,1]，我们选择s=5s=5，那么线段将是：[1,5][1,5]，[2,5][2,5]，[5,5][5,5]，[5,7][5,7]，[1,5][1,5]。各点的幂为：f1=2,f2=3,f3=3,f4=3,f5=5,f6=1,f7=1,f8=0,…,f109=0f_1=2, f_2=3, f_3=3, f_4=3, f_5=5, f_6=1, f_7=1, f_8=0, \dots, f_{10^9}=0。他们的总和是2+3+3+3+5+1+1=182+3+3+3+5+1+1=18。

思路

因为点的顺序不影响答案，可以先对x数组排序，例如样例里面的

1 1 2 5 7

现在计算5这个点：

如果按照题目里面的计算方式太复杂，可以考虑计算长度，例如区间[1,5][1,5]就是把区间1-5的点全部加1，最后再统计每个点的权值，

可以转换为计算这个区间的长度即可。

image-20230808130758728
image-20230808130758728

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<pair<int, int>> a(n + 1);
    vector<int> pre(n + 10), suf(n + 10);
    for (int i = 1; i <= n; i++) cin >> a[i].first, a[i].second = i;
    std::sort(a.begin() + 1, a.end());
    for (int i = 1; i <= n; i++) pre[i] = pre[i - 1] + a[i].first;
    for (int i = n; i >= 1; i--) suf[i] = suf[i + 1] + a[i].first;
    vector<int> res(n + 10);
    for (int i = 1; i <= n; i++) {
        int t = 1;
        t += a[i].first * (i - 1) + (i - 1) - pre[i - 1];
        t += suf[i + 1] + (n - i) - a[i].first * (n - i);
        res[a[i].second] = t;
    }
    for (int i = 1; i <= n; i++) cout << res[i] << " \n"[i == n];


}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

F. Sum and Product

题目

您有一个长度为nn的数组aa。

你的任务是回答qq个查询：给定x,yx,y，找到ai+aj=xa_i + a_j = x和ai⋅aj=ya_i \cdot a_j = y同时存在的ii和jj（1<=i<j<=n1 <= i < j <= n）对的数量。

也就是说，对于数组[1,3,2][1,3,2]并要求x=3,y=2x=3,y=2，答案是11：

  • i=1i=1和j=2j=2失败，因为1+3=41 + 3 = 4而不是3,3,，也是1⋅3=31 \cdot 3=3而不是22；
  • i=1i=1和j=3j=3满足两个条件；
  • i=2i=2和j=3j=3失败，因为3+2=53 + 2 = 5而不是3,3,，也是3⋅2=63 \cdot 2=6而不是22；

思路

可以先用map记录每个数字出现的次数

a[i]+a[j]=xa[i]+a[j]=x

a[i]∗a[j]=ya[i]*a[j]=y

可以把a[i],a[j]a[i],a[j]看成是方程t2−xt+y=0t^2-xt+y=0的两个解，这一步可以使用韦达定理，或者直接把a[i]=y/a[j]a[i]=y/a[j]带入第一个式子计算得到

韦达定理：ax2+bx+c=0ax^2+bx+c=0如果有解，则满足

x1+x2=−bax_1+x_2=-\frac{b}{a}

x1∗x2=cax_1*x_2=\frac{c}{a}

于是题目就转换为求解满足方程的解有多少组

delta=b2−4ac=x2−4ydelta=b^2-4ac=x^2-4y

  • 如果delta<0delta<0方程无解

  • 如果delta=0delta=0,方程有两个相同的解x1=x2x1=x2，此时只需要从map中选择两个=x1=x_1的数，即Ccnt2C_{cnt}^2(cnt为=x1的个数)

  • 如果delta>0delta>0,需要判断是否有两个不同的整数解，x=x+−delta2x=\frac{x+-\sqrt{delta}}{2},判断是否为整数，为答案的贡献为cnt1∗cnt2cnt1*cnt2

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

void solve() {
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) cin >> a[i];
    std::sort(a.begin() + 1, a.end());
    map<int, int> mp;
    for (int i = 1; i <= n; i++) mp[a[i]]++;
    int q;
    cin >> q;
    while (q--) {
        int x, y;
        cin >> x >> y;
        int delta = x * x - 4 * y;
        if (delta < 0) {
            cout << 0 << endl;
        } else if (delta == 0) {
            cout << mp[x / 2] * (mp[x / 2] - 1) / 2 << " ";
        } else {
            int sq = sqrt(delta);
            if (sq * sq != delta) {
                cout << 0 << " ";
            } else {
                if ((x + sq) % 2 != 0 || (x - sq) % 2 != 0) {
                    cout << 0 << " ";
                } else {
                    int x1 = (x + sq) / 2;
                    int x2 = (x - sq) / 2;
                    cout << mp[x1] * mp[x2] << " ";
                }
            }
        }
    }
    cout << endl;


}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}

G. Counting Graphs

题目

给定一棵由nn个顶点组成的树。树是无环的连通无向图。树的每条边都有其重量，wiw_i。

您的任务是计算满足所有四个条件的不同图表的数量：

1、图不存在自环和重边。
2、图边的权重为整数且不超过SS。
3. 该图恰好有一个 最小生成树open in new window。
4. 图的最小生成树是给定的树。

如果两个图的边集不同，则考虑到边的权重，则认为两个图不同。

答案可以很大，输出对998244353998244353取模。

思路

假设现在已经有了一个最小生成树，我们现在考虑要往上面进行加边操作，显然这条加的边一定是要比两个点x,yx,y之前的权值要大，否则最小生成树就可以选择刚刚加的这条边，那么最小生成树就要变了。因为边的权值上限为SS,因此加的边的取值范围为w～Sw～S，即有S−w+1S-w+1中选择

模拟克鲁思卡尔算法求最小生成树的过程，对于两个点x,yx,y,如果他们不在同一个集合，假设左边xx集合的大小为s1s_1,yy集合的大小为s2s_2,显然我可以从xx里面任意选一个点，从yy里面任意选一个点，然后这两个点之间可以加任意一条w～Sw～S的边，都不会影响到最小生成树。

选点的组合有s1∗s2−1s1*s2-1个组合,，每个组合都可以选择S−w+1S-w+1个边，方案数为：(S−w+1)s1∗s2−1(S-w+1)^{s1*s2-1}

S1*s2-1的减1是因为x和y这两个点是最小生成树的点，他们之间已经有一条边为w了，不可以再加边了，否则就是重边了

代码

#include <bits/stdc++.h>

#define int long long
#define yes cout << "YES" << endl;
#define no cout << "NO" << endl;
#define IOS cin.tie(0), cout.tie(0), ios::sync_with_stdio(false);
#define cxk 1
#define debug(s, x) if (cxk) cout << "#debug:(" << s << ")=" << x << endl;
using namespace std;

const int mod = 998244353;

struct DSU {
    std::vector<int> f, siz;

    DSU(int n) {
        f.resize(n + 1);
        siz.resize(n + 1);
        for (int i = 1; i <= n; i++) {
            f[i] = i;
            siz[i] = 1;
        }
    }

    int find(int x) {
        if (x != f[x]) f[x] = find(f[x]);
        return f[x];
    }

    bool same(int x, int y) {
        return find(x) == find(y);
    }

    bool merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x == y) {
            return false;
        }
        siz[x] += siz[y];
        f[y] = x;
        return true;
    }

    int size(int x) {
        return siz[find(x)];
    }
};

int qmi(int a, int b) {
    int res = 1;
    while (b) {
        if (b & 1) res = res * a % mod;
        a = a * a % mod;
        b >>= 1;
    }
    return res;
}

void solve() {
    int n, s;
    cin >> n >> s;
    vector<array<int, 3>> edge(n - 1);
    for (int i = 0; i < n - 1; i++) cin >> edge[i][0] >> edge[i][1] >> edge[i][2];
    sort(edge.begin(), edge.end(), [](array<int, 3> a, array<int, 3> b) { return a[2] < b[2]; });
    DSU dsu(n);
    int res = 1;
    for (auto [x, y, w]: edge) {
        int s1 = dsu.size(x), s2 = dsu.size(y);
        res = (res * qmi(s + 1 - w, s1 * s2 - 1)) % mod;
        dsu.merge(x, y);
    }
    cout << res << endl;
}

signed main() {
    IOS
#ifndef ONLINE_JUDGE
    freopen("../test.in", "r", stdin);
    freopen("../test.out", "w", stdout);
#endif
    int _ = 1;
    cin >> _;
    while (_--) solve();
    return 0;
}
上次编辑于:
贡献者: yunfeidog