树链剖分

OI Wiki [视频链接](https://www.bilibili.com/video/BV1tY4y1G7em/?spm_id_from=333.999.0.0&vd_source=c473bb1aae89eee47588dfc50fe8dc40重链剖分可以将树上的任意一条路径划分成不超过$O(logn)$条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 LCA 为链的一个端点)

重链剖分可以将树上的任意一条路径划分成不超过$O(logn)$条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 LCA 为链的一个端点)。

重链剖分还能保证划分出的每条链上的节点 DFS 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。

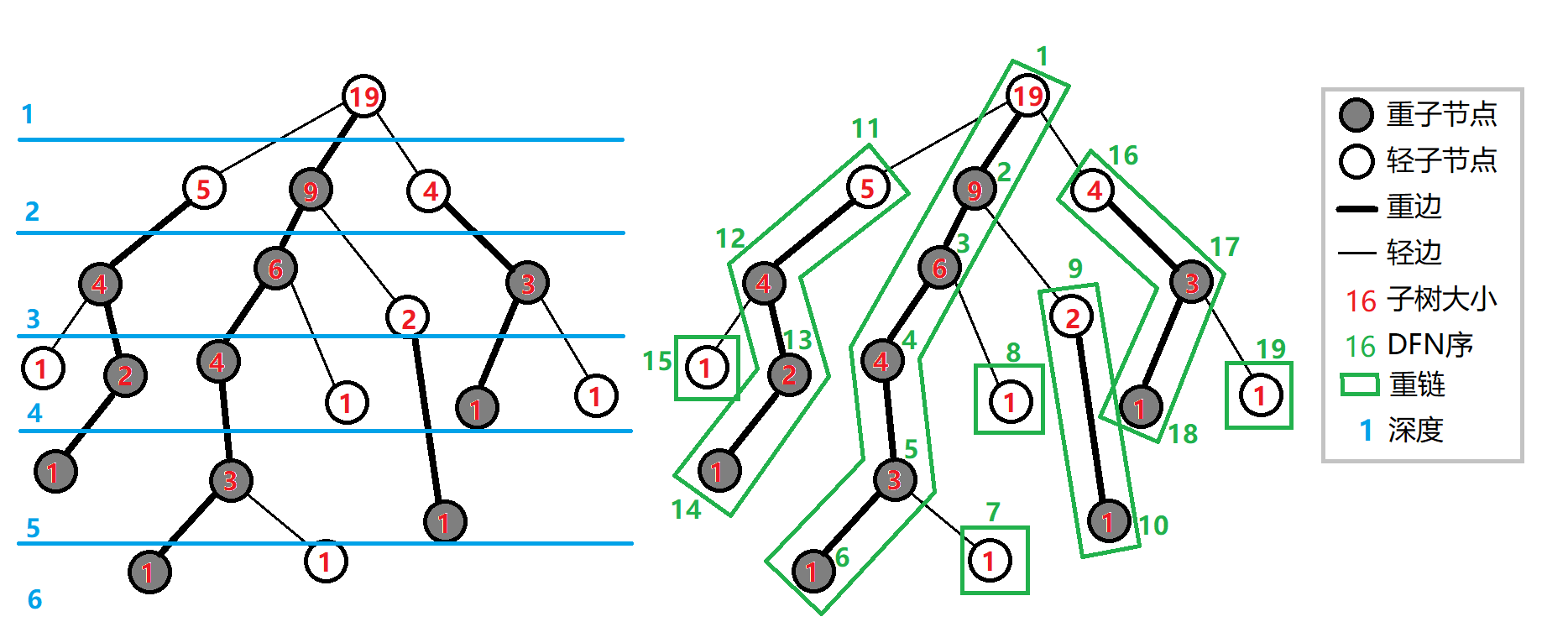
一些重要的概念

• 重儿子：父节点的所有儿子中子树节点数目最多的结点

• 轻儿子：父节点中除重儿子以外的儿子

• 重边：父节点喝重儿子连成的边

• 轻边：父节点和轻儿子连成的边

• 重链：由多条重边链接而成的路径

性质：

1. 整棵树会被剖分成若干条重链
2. 轻儿子一定是每条重链的顶点
3. 任意一条路径被分成不超过$logn$条链

在代码中的含义

• fa[u]表示存u的父节点
• dep[u]存u的深度
• son[u]存u的重儿子
• sz[u]存以u为根的子树的节点数
• top[u]存u所在重链的顶点
• dfs1(int u,int father) u为当前节点，father为父节点，该函数为了求出fa,dep,son数组
• dfs2(int u,int t)u为当前节点，t为链头，该函数为了求出top数组

最近公共祖先(LCA)

OJ

  // 树链剖分模板（轻重链剖分）
  #include <bits/stdc++.h>
  #define int long long
  using namespace std;
  const int N = 5e5 + 10;

  int n, m, root;
  vector<int> e[N];  // 存储树的边
  int fa[N], son[N], dep[N],sz[N];  // 分别为父节点、重儿子、深度、以该点为根的子树大小
  int top[N];  // 当前节点所在重链的顶部

  void dfs1(int u, int father) {  // 第一次dfs，确定重儿子和子树大小
      fa[u] = father, dep[u] = dep[father] + 1, sz[u] = 1;  // 记录父节点、深度、以u为根的子树大小
      for (int v : e[u]) {
          if (v == father)
              continue;            // 防止向上找到父亲节点
          dfs1(v, u);              // dfs该儿子节点
          sz[u] += sz[v];          // 维护以u为根的子树大小
          if (sz[son[u]] < sz[v])  // 更新重儿子
              son[u] = v;
      }
  }

  void dfs2(int u, int t) {  // 第二次dfs，确定每个节点所在重链的顶部
      top[u] = t;            // 当前节点所在重链的顶部为t
      if (!son[u]) return;       // 没有重儿子，直接退出
      dfs2(son[u], t);  // 递归处理重儿子
      for (int v : e[u]) {
          if (v == fa[u] || v == son[u])
              continue;  // 处理轻儿子时跳过重儿子和父亲节点
          dfs2(v, v);    // 搜轻儿子，并以轻儿子为顶部继续dfs
      }
  }

  int lca(int x, int y) {  // 查询x、y两个点的LCA（最近公共祖先）
      while (top[x] !=top[y]) {  // 如果x、y不在同一条重链上，则将深度较大的节点往上跳
          if (dep[top[x]] < dep[top[y]])  // 保证x节点所在的重链深度不小于y节点所在的重链深度
              swap(x, y);
          x = fa[top[x]];
      }
      return dep[x] < dep[y] ? x : y;  // 最终结果为x、y所在链的最近公共祖先，即depth更浅的那个节点
  }

  void solve() {
      cin >> n >> m >> root;
      for (int i = 1; i <= n - 1; i++) {
          int x, y;
          cin >> x >> y;
          e[x].push_back(y);  // 添加树的边，注意无向图要存两遍
          e[y].push_back(x);
      }
      dfs1(root, 0);  // 执行dfs1，确定重儿子和以该点为根的子树大小
      dfs2(root, root);  // 执行dfs2，确定每个节点所在重链的顶部
      while (m--) {
          int x, y;
          cin >> x >> y;
          cout << lca(x, y) << endl;  // 查询x、y的LCA
      }
  }

  signed main() {
  #ifndef ONLINE_JUDGE
      freopen("../test.in", "r", stdin);
      freopen("../test.out", "w", stdout);
  #endif
      int _ = 1;
      while (_--)
          solve();
      return 0;
  }