有向图的强联通分量(SCC)Tarjan算法O(n+m)
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
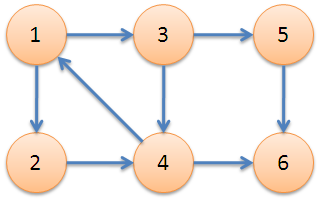
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
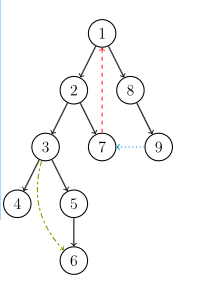
DFS生成树:
大约 7 分钟
强连通分量(Strongly Connected Components,SCC)的定义是:极大的强连通子图。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

DFS生成树:

给定一个有向无环图(DAG),排出所有顶点的一个序列A满足:对于图中每条有向边(x,y),x在A中都出现在y之前,则A是该图中的顶点的一个拓扑序
拓扑排序可以判断 有向图中是否有环 ,可以生成拓扑序列
算法流程:核心用队列维护一个入度为0的节点的集合。
Dijkstra算法是单源最短路算法,是用来求一个点到其他所有点点最短距离,使用小根堆优化后时间复杂度大概为Omlogn
注意:不可以解决存在负权边的问题
OI Wiki [视频链接](https://www.bilibili.com/video/BV1tY4y1G7em/?spm_id_from=333.999.0.0&vd_source=c473bb1aae89eee47588dfc50fe8dc40重链剖分可以将树上的任意一条路径划分成不超过$O(logn)$条连续的链,每条链上的点深度互不相同(即是自底向上的一条链,链上所有点的 LCA 为链的一个端点)
全源最短路算法,可以求任意两个点之间的最短路,是一种动态规划算法,也称为插点法
https://www.acwing.com/problem/content/description/856/
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,边权可能为负数。